Evidence for chiral supercurrent in quantum Hall Josephson junctions

Hybridizing superconductivity with the quantum Hall (QH) effect holds promise for designing circuits that manipulate non-Abelian states for topological quantum computation. Despite experimental progress, concrete evidence for a chiral QH Josephson junction—key to coherent superconducting QH circuits—remains elusive. Its expected signature is a chiral supercurrent in QH edge channels with a 2ϕ0 magnetic flux periodicity (ϕ0 = h/2e, where h is Planck’s constant and e the electron charge). We demonstrate chiral supercurrent in ultra-narrow Josephson junctions in encapsulated graphene nanoribbons, observed up to 8 T, carried by the spin-degenerate edge channel of the QH plateau (resistance h/2e2 ≈ 12.9 kΩ). The supercurrent shows reproducible 2ϕ0-periodic oscillations at a constant filling factor when the QH edge channel loop area is constant, with a magnetic-length correction. By varying junction geometry, we find that reducing the superconductor/normal interface length is essential for measurable supercurrent on QH plateaus, aligning with theories predicting dephasing along the superconducting interface. These findings advance the exploration of QH-based superconducting devices that host non-Abelian Majorana and parafermion zero modes.
Probing the fractional quantum Hall phases in valley-layer locked bilayer MoS2

Semiconducting transition-metal dichalcogenides (TMDs) exhibit high mobility, strong spin–orbit coupling, and large effective masses, which simultaneously leads to a rich wealth of Landau quantizations and inherently strong electronic interactions. How- ever, in spite of their extensively explored Landau levels (LL) structure, probing electron correlations in the fractionally filled LL regime has not been possible due to the difficulty of reach- ing the quantum limit. Here, we report evidence for fractional quantum Hall (FQH) states at filling fractions 4/5 and 2/5 in the lowest LL of bilayer MoS2, manifested in fractionally quantized transverse conductance plateaus accompanied by longitudinal re- sistance minima. We further show that the observed FQH states sensitively depend on the dielectric and gate screening of the Coulomb interactions. Our findings establish a new FQH experi- mental platform which are a scarce resource: an intrinsic semicon- ducting high mobility electron gas, whose electronic interactions in the FQH regime are in principle tunable by Coulomb-screening engineering, and as such, could be the missing link between atom- ically thin graphene and semiconducting quantum wells.
Tangent Fermions: Dirac or Majorana Fermions on a Lattice Without Fermion Doubling
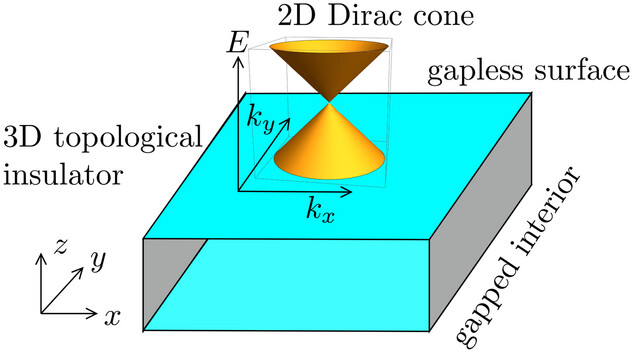
Methods for discretizing the Hamiltonian of topological insulators and superconductors, while preserving the topological protection of massless excitations (Dirac or Majorana fermions), are reviewed. The method of tangent fermions, introduced by Richard Stacey, is highlighted as especially well-suited for this. Tangent fermions propagate on a space-time lattice with a tangent dispersion, avoiding fermion doubling—a lattice artifact that compromises topological protection—while maintaining the symmetries of the Dirac Hamiltonian. Although the discretized Hamiltonian is nonlocal, as required by the fermion-doubling no-go theorem, it can be reformulated into a generalized eigenproblem that is local in space and time. Applications include Dirac fermion Klein tunneling, disorder resistance, the anomalous quantum Hall effect, and the Majorana fermion thermal metal.
Transport signatures of Van Hove singularities in mesoscopic twisted bilayer graphene

Magic-angle twisted bilayer graphene exhibits quasiflat low-energy bands with Van Hove singularities close to the Fermi level. These singularities play an important role in the exotic phenomena observed in this material, such as superconductivity and magnetism, by amplifying electronic correlation effects. In this work, we study the correspondence of four-terminal conductance and the Fermi surface topology as a function of the twist angle, pressure, and energy in mesoscopic, ballistic samples of small-angle twisted bilayer graphene. We establish a correspondence between features in the wide-junction conductance and the presence of Van Hove singularities in the density of states. Moreover, we identify additional transport features, such as a large, pressure-tunable minimal conductance, conductance peaks coinciding with nonsingular band crossings, and unusually large conductance oscillations as a function of the system size. Our results suggest that twisted bilayer graphene close the magic angle is a unique system featuring simultaneously large conductance due to the quasiflat bands, strong quantum nonlinearity due to the Van Hove singularities, and high sensitivity to external parameters, which could be utilized in high-frequency device applications and sensitive detectors.
Emerging quantum hybrid systems for non-Abelian-state manipulation

The non-Abelian state has garnered considerable interest in the field of fundamental physics and future applications in quantum computing. In this review, we introduce the basic ideas of constructing the non-Abelian states in various systems from 1D to 3D and discuss the possible approaches to detect these states, including the Majorana bound states in a hybrid device and the v = 5/2 state in a fractional quantum Hall system.
Chiral limit and origin of topological flat bands in twisted transition metal dichalcogenide homobilayers

The observation of zero field fractional quantum Hall analogs in twisted transition metal dichalcogenides (TMDs) asks for a deeper understanding of what mechanisms lead to topological flat bands in two-dimensional heterostructures, and what makes TMDs an excellent platform for topologically ordered phases, surpassing twisted bilayer graphene. To this aim, we explore the chiral limits of massive Dirac theories applicable to C3-symmetric moiré materials, and show their relevance for both bilayer graphene and TMD homobilayers. In the latter, the Berry curvature of valence bands leads to relativistic corrections of the moiré potential that promote band flattening, and permit a limit with exactly flat bands with nonzero Chern number. The relativistic corrections enter as a layer-orbit coupling, analogous to spin-orbit coupling for relativistic Dirac fermions, which we show is non- negligible on the moiré scale. The Berry curvature of the TMD monolayers therefore plays an essential role in the flattening of moiré Chern bands in these heterostructures.
Fractional Chern insulators versus nonmagnetic states in twisted bilayer MoTe2

Fractionally filled Chern bands with strong interactions can lead to fractional Chern insulator (FCI) states, akin to the fractional quantum Hall effect but without magnetic fields. Recent experiments have observed FCIs at ν = −2/3 and Chern insulators (CIs) at ν = −1 in twisted bilayer MoTe2, yet puzzlingly, nonmagnetic or weakly magnetic states are found at ν = −1/3 and −4/3, without FCIs. To address this, we perform Hartree-Fock and exact diagonalization calculations using the MoTe2 moiré model and parameter values from literature. We test whether these can reproduce the nonmagnetic states at ν = −1/3 and −4/3, along with the FCI at ν = −2/3 and CI at ν = −1. Including remote bands and focusing on relevant twist angles, we find that parameters proposed by Wang et al. [arXiv:2306.02501] nearly match the experimental observations, though FCIs at ν = −1/3 remain dominant, and a larger dielectric constant ε > 10, higher than the typical hexagonal boron nitride (h-BN) ε ∼ 6, is needed. Our results highlight the role of remote bands in determining magnetic orders and provide a foundation for further exploration of the phase diagram.


